Home - StackOverflow

0

W3spoint99Begginer

Asked: December 30, 2024In: Biology

Diversity In The Living World (Class 11 – Biology)

0

Explain Diversity In The Living World (Class 11 – Biology) – Notes.

Saralyn Begginer
Added an answer on December 30, 2024 at 7:02 am
This answer was edited.
Diversity In The Living World Each residing life form will in general share highlights like development, upkeep of homeostasis, propagation, utilization of energy, adaption, and so forth. These highlights help to recognize various species and furthermore prove to be useful in laying out a connectionRead more

Diversity In The Living World

Each residing life form will in general share highlights like development, upkeep of homeostasis, propagation, utilization of energy, adaption, and so forth. These highlights help to recognize various species and furthermore prove to be useful in laying out a connection between organic entities with a typical hereditary part.

Biodiversity: Biodiversity is every one of the various types of life you’ll track down in one region — the range of creatures, plants, growths, and even microorganisms like microbes that make up our normal world. Every one of these animal categories and living beings cooperates in environments, similar to a multifaceted web, to keep up with equilibrium and back life. Biodiversity upholds everything in nature that we want to get by food, clean water, medication, and asylum.

Taxonomy: Taxonomy is the area of science that manages the recognizable proof, terminology, and grouping of creatures.

Identification: Identification is the acknowledgment of the fundamental person of a life form.

Nomenclature: Nomenclature is the naming of life forms. Latinized names are utilized to allude to various types of plants and creatures.

Features of Living World

Development: The expansion in cells’ number and mass through cell division.

Material sense: It is the capacity to detect the climate.

Digestion: A progression of biochemical responses happening in the body to shape and change substance organization.

Proliferation: The method involved creating posterity and proceeding with the progeny.

Organization: The very characterizing qualities of every living organic entity.

Cognizance: The feeling of monitoring one’s environmental factors, activities, and aims.

Diversity in the Living World

The world is overwhelmed by plenty of living organic entities living in the land, water, ice, sweets, and so forth. Each living organic entity is one of a kind of structure, body capabilities, hereditary make-up, etc. The living life forms found in various natural surroundings have different primary organs or capabilities created according to the states of their environment. Organic entities have advanced to adjust to their evolving surroundings. Various sorts and classes of life forms possessing various conditions are known as biodiversity. Districts that are warm and damp have more different organic entities and are called super biodiversity.

People have advanced from primates. However, presently they don’t appear to be comparative in any capacity. Likewise, every individual is not quite the same as the other. Each individual has an alternate skin tone, hair tone, and eyes, and generally significant of everything is hereditary cosmetics. And that implies that the qualities of each and every individual are unique.

In this manner, to recognize better, we have made gatherings of creatures that in some way seem to be comparative and have a few utilitarian and primary similitudes. This is known as order. There are different variables that impact the order of creatures. It is significantly done based on the accompanying models

Presence of core

Body plan which infers the make-up of cells or the presence of single or numerous cells

Food creation

Level of the association in groups of creatures completing photosynthesis

In creatures – an association of one’s body parts, advancement of body, particular organs for various capabilities, organs frameworks.

Classification System

The grouping of life forms is finished by two techniques. One is characterizing them into plants and creatures and the other one which is a five-realm framework is a more nitty-gritty and coordinated characterization of living beings:

Two-Kingdom Classification- It was proposed via Carolus Linnaeus. He ordered organic entities into two classifications, plants, and creatures.

Five-Kingdom Classification- It was proposed by Whittaker. He separated the life forms into five distinct classes.

Monera

Protista

Fungi

Plantae

Animalia

Hierarchy of Classification

Carolus Linnaeus additionally organized the organic entities into various scientific classifications at various levels. These scientific classifications in a chronic request are as per the following

Kingdom

Phylum

Class

Order

Family

Genus

Species

Characteristics of Five Kingdoms

Kingdom Monera

These are unicellular prokaryotes. The life forms come up short on the evident nucleus. They might contain a cell wall. They might be heterotrophic or autotrophic in nature. For instance Bacteria, Cyanobacteria.

Kingdom Protista

Protista are unicellular and eukaryotic organic entities go under this group. They display an autotrophic or heterotrophic method of nutrition. They show the presence of pseudopodia, cilia, or flagella for headway. For instance one-celled critter, paramecium.

Kingdom Fungi

These are multicellular, eukaryotic organisms. They have a saprophytic method of nourishment which includes chemoheterotrophic extracellular processing. The cell wall in these organic entities is comprised of chitin. They live in a cooperative relationship with blue-green growth. For instance Yeast, Aspergillus

Kingdom Plantae

These are multicellular, eukaryotic organisms. The cell mass of these creatures is comprised of cellulose. They are heterotrophs and set up their own food through photosynthesis. Kingdom Plantae is partitioned into Thallophyta, Bryophyta, Pteridophyta, Gymnosperms, and Angiosperms. For instance Pines, plants, palm trees, mango trees, and so on.

Kingdom Animalia

Kingdom Animalia is multicellular, eukaryotic living beings yet they don’t show the presence of cell walls. They are heterotrophs or creatures who can’t set up their own food. Both straightforward and complex life forms are found in this gathering and it’s an extremely general gathering of organisms. The organic entities are hereditarily diverse. They display an organ-framework level of organization. It is partitioned into various phyla like Porifera, Coelenterata, Echinodermata, Chordata, Annelids, and so on. For instance Earthworms, Hydra, and so on.

FAQs on Diversity In The Living World

Question 1: Why are living creatures arranged?

Answer:

A colossal assortment of plants, creatures, and organisms are tracked down on the planet. This multitude of living creatures varies in size, shape, variety, natural surroundings, and numerous different attributes. As there is an enormous number of living organic entities on the planet, concentrating on every one of them is unimaginable. Accordingly, researchers have concocted systems to arrange every single living creature. These strategies for arrangement depend on decisions and rules that permit recognizable proof, terminology, and lastly characterization of an organic entity.

Question 2: Why are the order frameworks changing occasionally?

Answer:

Huge quantities of plants, creatures, and microorganisms are tracked down on the planet. A significant number of these have been recognized by researchers while numerous new species are as yet being found all over the planet. In this manner, to order these newfound species, new frameworks of the arrangement must be determined from time to time. This makes the necessity to change the current frameworks of order.

Question 3: What various measures could you decide to group individuals that you meet frequently?

Answer:

The different standards that might be decided to arrange individuals whom we meet frequently incorporate a way of behaving, geological area, morphology, relatives, family members, companions, and so forth.

Question 4: What do we gain from distinguishing proof of people and the populace?

Answer:

The information on attributes of an individual or its entire populace helps in recognizable proof of similitudes and dissimilarities among the people of a comparative kind or between various sorts of life forms. It assists us with grouping living beings into different classes relying on these similitudes and dissimilarities.

Question 5: Given underneath is the logical name of Mango. Recognize the accurately composed name. Mangifera Indica

Answer:

In the binomial arrangement of terminology, the conventional name of an animal group generally begins with a capital letter though the particular name begins with a little letter. Accordingly, the right logical name for Mango is Mangifera indica.

See less
0

Share
Share

Share on Facebook

Share on Twitter

Share on LinkedIn

Share on WhatsApp

Report

0

W3spoint99Begginer

Asked: January 17, 2025In: Physics

System of Units (Class 11 – Physics)

0

Please Explain System of Units (Class 11 – Physics).

Saralyn Begginer

Added an answer on January 17, 2025 at 3:25 pm

Measurement forms the fundamental principle to various other branches of science, that is, construction and engineering services. Measurement is defined as the action of associating numerical with their possible physical quantities and phenomena. Measurements find a role in everyday activities to aRead more

Measurement forms the fundamental principle to various other branches of science, that is, construction and engineering services. Measurement is defined as the action of associating numerical with their possible physical quantities and phenomena. Measurements find a role in everyday activities to a large extent. Therefore, it is necessary to study and explore the associated elements along with their theoretical foundations, conditions as well as limitations. It defines the units to be chosen for the measurement of various commodities. It also caters to the comparison of plausible units with the ones already existing of a similar kind.

Measurement defined the new standards as well as form transductions for the quantities which do not have any possible access for direct comparison. These physical quantities can be converted into analogous measurement signals.

Measurements may be made by unaided human senses, generally termed as estimates. It can also be estimated by the use of instruments, which may range in complexity from simple rules for measuring lengths to highly complex analogous systems to handle and design the commodities beyond the capabilities of the senses. Thus, the measurements may range from buying some quantity of milk (in L) or to the highly complex mechanisms, such as radio waves from a distant star or the nuclear bomb radiations. Therefore, we can consider that a measurement, always involves a transfer of energy or interaction between the object and the observer or observing instrument.

Measurement of Height of a person

Unit

The unit of a specified physical quantity can be considered as an arbitrarily chosen standard that can be used to estimate the quantities belonging to similar measurements. The units are well accepted and recognized by the people and well within all guidelines.

A physical quantity is measured in terms of the chosen standards of measurement.

The chosen standard is recognized as the unit of that corresponding physical quantity. A standard unit, in short, is a definite amount of a physical quantity. These standard units can be quickly reproduced to create a wide variety of units and are internationally accepted and accessible.

The measurement of any physical quantity is based on a formula, nu,

where, n = numerical value of the measure of the quantity,

u = unit of the quantity.

Standard

The actual physical embodiment of the unit of a physical quantity is termed as a standard of that physical quantity. The standard is expressed in terms of the numerical value (n) and the unit (μ).

Measurement of physical quantity = Numerical value × Unit

For example: Length of a rod = 12 m. Here 12 is its numerical segment and m (meter) is the unit.

Fundamental Units

Fundamental units are elementary in nature, that is, they can be expressed independently without any dependence on any other physical quantity. This implies that it is not possible to resolve it further in terms of any other physical quantity. It is also termed as a basic physical quantity. Fundamental quantities have their own values and units.

Fundamental Quantities	Fundamental Units	Symbol
Length	meter	m
Mass	kilogram	kg
Time	second	s
Temperature	kelvin	k
Electric current	ampere	A
Luminous intensity	candela	cd
Amount of substance	mole	mol

Supplementary Fundamental Units

There are two other supplementary fundamental units, namely Radian and steradian are two supplementary which measures plane angle and solid angle respectively.

Supplementary Fundamental Quantities	Supplementary Unit
Plane angle	radian
Solid angle	steradian

Radian (rad)
One radian is equivalent to an angle subtended at the center of a circle by an arc of length equal to the radius of the circle. It is the unit represented for the plane angle.

θ = 1 radian

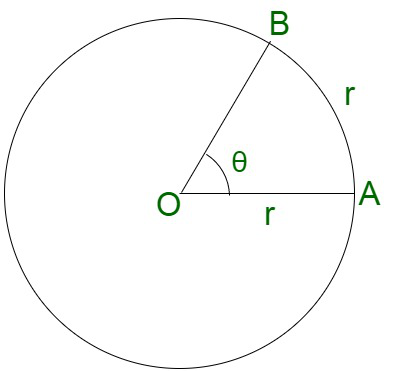
$dθ=\left(\frac{ds}{r}\right)\ radian$

Steradian (sr)
One steradian is equivalent to the solid angle subtended at the center of a sphere by its surface. Its area is equivalent to the square of the radius of the sphere.It is the unit represented for the solid angle. Solid angle in steradian,

Ω = 1 steradian

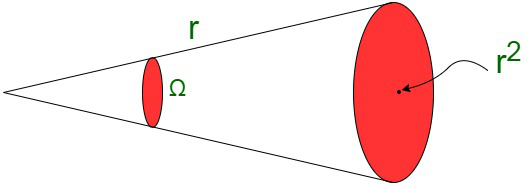
$dΩ =\frac{Area\ cut\ out\ from\ the\ surface\ of\ sphere}{(Radius)^2}\\ dΩ =\left(\frac{dA}{r^2}\right)\ steradian$

Properties of Fundamental Units

Any standard unit should have the following two properties:

Invariability
The standard unit must be invariable. Thus, defining distance between the tip of the middle finger and the elbow as a unit of length is not invariable.
Availability
The standard unit should be easily made available for comparing with other quantities.

The seven fundamental units of S.I. have been defined as under.

Meter (m)
Defined as 1650763.73 times the wavelength, in vacuum of the orange light emitted in transition from 2p¹⁰ to 5d⁵.
Kilogram (kg)
Defined as the mass of a platinum-iridium cylinder kept at Serves.
Second (s)
Time taken by 9192631770 cycles of the radiation from the hyperfine transition in cesium – 133 when unperturbed by external fields.
Ampere (A)
The constant current which, if maintained in each of two infinitely long, straight, parallel wires of negligible cross-section placed 1 m apart, in vacuum, produces between the wires a force of 2×10^-7 newton per meter length of the wires.
Kelvin (K)
Temperature is measured with absolute zero as the zero and the triple point of water as the upper fixed point on the thermodynamic scale. The interval is divided into 273.15 divisions and each division is considered to be unit temperature.
Candela (cd)
The luminous intensity in the perpendicular direction of a surface of $\frac{1}{600000}$ square meter of a full radiator at the temperature of freezing platinum under a pressure of 101325 newtons per square meter.
Mole (mol)
The mole is the amount of any substance which contains as many elementary entities as there are atoms in 0.012 kg of the carbon isotope $\frac{12}{6}$ C.

Derived units

The derived units are in usage for the commodities where the units are obtained from a combination of fundamental units. Derived units are sometimes assigned names. For instance, the S.I unit of force is kg ms^-2, termed as Newton (N). The unit of power is kg m² s^-3 , termed as watt (W).

Steps to find Derived Units

Fetch the formula for the quantity whose unit is to be derived.
Substitute units of all the involved quantities. The chosen units should all belong to one system on units in their fundamental or standard form.
Simplify for the derived unit of the quantity to compute its final unit.

Example: Compute the unit of velocity.

Since, we know velocity is a derived quantity, obtained from distance and time(fundamental quantities).

Mathematically ,

velocity = displacement/time

S.I. unit of velocity = $\frac{S.I.\ unit\ of\ displacement}{ S.I.\ unit\ of\ time}$ = m/s

Thus S.I. unit of velocity is m/s.

Some Important derived units

Some of the derived units have been given specific names, depending on the increase in their usage , though they are not recognized in S.I units.

Micron (mm) = 10^-6 m
Angstrom (Å) = 10^-10 m
Fermi (fm) = 10^-15 m
Barn (b) = 10^-28 m²

Systems of Units

Any system of units contains the entire set of both fundamental as well as derived units, for all kinds of physical quantities. The preferred system of units are the following :

CGS System (Centimeter Gram Second)
The unit of length is centimeter, the unit of mass is gram and the unit of time is second according to the guidelines of this system.
FPS System (Foot Pound Second)
The unit of length is foot, the unit of mass is pound and the unit of time is second according to the guidelines of this system.
MKS System (Meter Kilogram Second)
The unit of length is meter, the unit of mass is kilogram and the unit of time is second according to the guidelines of this system.
SI System
The System Internationale d’ Units, that is S.I system contains seven fundamental units and two supplementary fundamental units.

Note:

While computation of values for any physical quantity, the units for the involved derived quantities are treated as algebraic quantities till the desired units are obtained.

Advantages of S.I Unit System

The S.I unit of measurement is preferred over other units of measurement, because,

It is internationally accepted.
It is a metric system.
It is a rational and coherent unit system,
Easy conversion between CGS and MKS systems of units.
Uses decimal system, which is easy to understand and apply.

Other Important Units of Length

The distances can be infinitely larger in magnitude, which cannot be depicted in terms of meters or kilometers. For instance, the distances of planets and stars etc. Therefore, it is necessary to use some larger units of length such as ‘astronomical unit’, ‘light year’, parsec’ etc. while making such calculations, some of which are :

Astronomical Unit – The average separation between the Earth and the sun.
1 AU = 1.496 x 10¹¹ m.
Light Year – The distance travelled by light in vacuum in one year.
1 light year = 9.46 x 10¹⁵ m.
Parsec – The distance at which an arc of length of one astronomical unit subtends an angle of one second at a point.
1 parsec = 3.08 x 10¹⁶ m
Fermi – Size of a nucleus is expressed in ‘fermi’.
1 fermi = If = 10^-15 m
Angstrom – Size of a tiny atom
1 angstrom = 1A = 10^-10 m

Sample Problems

Problem 1. Convert the unit of G, which is gravitational constant, G = 6.67 x 10^-11Nm²/kg² in CGS system.

Solution:

Since, we have

G = 6.67 x 10-¹¹ Nm²/kg²

Converting kg into grams, 1 kg = 1000 gms

= 6.67 x 10-¹¹ x 10⁸ x 10³ cm³/g¹ s²

= 6.67 x 10⁸ cm3/g1 s2

Problem 2. Name the S.I units of the following commodities :

a. Pressure

b. Solid angle

c. Luminous intensity.

Solution:

a. Pascal

b. Steradian

c. Candela

Problem 3. Derive the S.I unit of latent heat.

Solution:

Latent heat = $\frac{Heat energy}{Mass}$

$Latent\space Heat = \frac{Q}{m} \\ =\frac{ kg m^2 s^{-2}}{kg} \\ = m^2 s^{-2}$

Problem 4: How are A⁰and A.U related?

Solution:

Describing both quantities in terms of meters,

A^o = 10^-10m

and 1 A.U. = 1.49610¹¹m.

Therefore,

1 A.U. = 1.496 x 10¹¹x 10¹⁰A⁰

1 A.U = 1.496 x 10²¹ A⁰

Problem 5: Describe 1 light-year in meters.

Solution:

A light-year is a distance travelled by light in 1 year with the speed of light :

= 9.46 x 10¹¹ m

See less

0

W3spoint99Begginer

Asked: January 17, 2025In: Physics

Length Measurement (Class 11 – Physics)

0

Please Explain Length Measurement (Class 11 – Physics).

Saralyn Begginer
Added an answer on January 17, 2025 at 3:25 pm
Previously, length was measured using units such as the length of a foot, the breadth of a palm, and so on. The ‘Cubit’ was one of the first means of measuring length. It is the length of the arm from the elbow to the tip of the fingers. These units vary from person to person, resulting in non-unifoRead more

Previously, length was measured using units such as the length of a foot, the breadth of a palm, and so on. The ‘Cubit’ was one of the first means of measuring length. It is the length of the arm from the elbow to the tip of the fingers. These units vary from person to person, resulting in non-uniform measures.

How can we know how far the moon is from the earth or how far the moon is from the sun? How did we determine the earth’s diameter? Measuring length isn’t always simple or easy. We’ll try to respond to these queries in the sections below. In addition, we will learn about the many methods for measuring length.

Length

The measurement or amount of anything from one end to other is referred to as length.

In other terms, it is the largest of the two or the highest of three geometrical form or item dimensions. The width and length of a rectangle, for instance, are its dimensions. Furthermore, under the International System of Quantities, length is a quantity with the dimension distance.

The meter, abbreviated as m, is the basic unit for length in the International System of Units (SI). The length or distance is measured in kilometers (km), meters (m), decimeters (dm), centimeters (cm), and millimeters (mm) in the metric system (mm). It is possible to convert quantities from meters to centimeters, kilometers to meters, centimeters to millimeters, and so on.

Measurement of Length

There were no modes of transportation available in ancient times. People used to travel on foot or by using animals to transport goods. Over time, the term “wheel” was coined. This signified a significant shift in human forms of transportation. Since then, new forms of transportation have been invented and improved regularly. The steam engine was created, and it had a great influence and was instrumental in shaping the world as we know it today.

As a result, transportation has a lengthy history. Did the folks have any idea how far they had to go? To go to any location, one must first determine how far away it is. This aids in deciding whether to walk, take the train, bus, or fly to that location. To determine how far apart two locations are, we must first determine the distance between them. But what exactly does measurement imply? What is the best way to measure a physical quantity? The comparing of an unknown amount to a known amount is known as measurement. A numerical number known as “magnitude” and a “unit” are used to indicate the outcome of the measurement. A ‘unit’ is a pre-determined unit of comparison against which other physical quantities are measured.

The length of the foot, the breadth of the palm, and other such quantities were used to measure the length in the past. The ‘Cubit’ was one of the first means of measuring length. It is the length of an arm measured from elbow to tips of fingers. These units varied from person to person, resulting in non-uniform measures. A set of standard units of measurement has been recognised all around the world to preserve uniformity in measurements.

The International System of Units (SI) is one of the most widely used measurement systems in the world. The basic unit of length in the SI system is the meter. The C.G.S. system is another system of units in which the centimeter is the basic unit of length.

Conventional Methods of Measurements

Historically, the human body served as the foundation for length units.

Inch: An inch is a unit of measurement that was once used to measure the length of little things such as the length of paper, the seam of cloth, and so on.

Foot: A foot is a unit of length that is commonly defined as 15.3 per cent of a human body’s height, with an average height of 160 cm. This unit differed from one location to the next and from one transaction to the next. The Romans and Greeks favored this unit, which was commonly used to compute the height of humans and livestock, the size of a piece of fabric, the size of a structure, and so on.

Cubit: A cubit is a unit of length based on the length of the forearm, which is commonly measured from the tip of the middle finger to the forearm’s length bottom of the elbow. The Egyptians and Mesopotamians favored this unit. Cubit rods have been unearthed among the ancient Egyptian civilization’s relics. These rods are typically 20 inches long and are split into seven palms, each of which is split into four fingers, which are further subdivided.

Yard: A yard is a measurement of distance based on human paces. It is usually measured in two cubits, which is around 36 inches.

Mile: A mile is equal to 1,000 paces, where a pace is equal to two steps and the walker returns to the same foot.

A foot is 12 inches long, and a yard is three feet long. It was simple to describe how distant the next village was and to determine if an object would fit through a doorway using these dimensions. These dimensions also made it easier for individuals to swap garments and wood.

Scale

Triangulation Method

Let’s take a closer look at what the triangulation approach entails. How might triangulation assist us in determining the distances between distant stars? The parallax approach makes use of the fact that a triangle may be entirely defined using only three parts. Triangulation is the process of determining the values of a triangle to determine an item’s position. Surveyors and architects frequently employ such techniques.

Triangulation is the method of identifying the location of a point by calculating the angles to it from two known sites rather than calculating distances directly.

Triangulation Example

Let’s put this into practice with a real-life scenario. How can we estimate a large object distance from any distance without actually measuring it? It may be measured using the triangulation method.

Triangulation Method of measurement

Let’s start by constructing a fixed baseline with two points AB.

The angle formed by point A concerning the object is denoted by α, whereas the angle formed by point B concerning the object is marked by β.

Now that we have the baseline AB and the angles, we can determine the remainder of the triangle’s attributes, such as the position of the third point, which is the object.

Parallax Method

The displacement or shift in the apparent location of an item when observed from two distinct points of view is known as parallax.

The two places of vision each have their own line of sight, and parallax is defined as half the angle between them. When you’re driving in a car and glance about, you’ll notice that items far away appear to move more slowly than items closer to you. This is the parallax effect. Because the parallax of nearby objects is greater than that of distant ones, the parallax may be utilised to measure distances.

When the phenomena of parallax is coupled with triangulation, the position of the item may be determined with great precision. The parallax method is commonly used by astronomers to determine the distances between stars.

Distance Measurement by Parallax Method

The principle of triangulation is used to the measuring of distance through parallax. We learned from triangulation that a triangle may be completely specified if two angles and sides are known.

The distance of a faraway star is being computed in the image below. The star closer to Earth than the farthest one gives the limited parallax value. By observing the star from two known places on Earth that form the triangle’s baseline, we may determine the value of the parallax angle.

Parallax Method

Let’s denote the parallax half-angle between two places on Earth ‘p.’ The radius of the Earth is the greatest value of ‘d,’ and the distance of the star may be considered to be just slightly more than that of the sun. Because the distance from the sun is several orders of magnitude lower than the radius of the Earth, the parallax angle we obtain is exceedingly modest.

Application

The distance to an object measured in parsecs (in terms of light speed) is equal to the reciprocal of parallax angle measured in arcseconds.

Relation between the distance of a star, and its parallax is given as:

D = 1 ⁄ p

where D is the distance of star and p is the parallax angle.

To solve the difficulty of tiny ratios, the parallax of a star is most commonly estimated using yearly parallax, which is defined as the difference in a star’s location as seen from the Earth and the Sun. Instead of using the Earth’s radius as a fixed baseline, the radius of the Earth’s revolution around the Sun is used, which increases the size of the baseline and hence the top angle, making it simpler to measure.

However, for any celestial objects near to the Earth, we can consider the diameter of the Earth as a baseline, and the distance of any celestial objects is given as:

x = b ⁄ θ

where x is the distance of the object from the Earth, b is the baseline or diameter of the Earth and θ is the angle subtended by the object.

Sample Problems

Problem 1: If a person covers 1.5 yards in one step, how much distance will he cover in 30 steps?

Solution:

Given:

Total number of steps, n = 30

Value of 1 step, d = 1.5 yards

Total distance covered by the person, D = n d

= 30 × 1.5 yard

= 45 yards

Hence, the distance covered by the person is 45 yards.

Problem 2: Astronomers apply which method to determine how far away a star is?

Answer:

Astronomers use parallax to calculate the distance between stars. Trigonometric parallax is another name for parallax.

Problem 3: What is parallax?

Answer:

The two items appear to be coincident when seen in a straight line. There is a relative displacement between the things if they are at separate locations and the eye is shifted sideways. The closer item travels in the opposite direction from the eye, whereas the further object travels in the same direction.

When two things are perceived in a straight line and the eye is shifted to the side, this is referred to as parallax.

Problem 4: What was the conventional method of measuring the length?

Answer:

The length was measured in history with the help of human body. These were based on the several methods like distance from tip of middle finger to bottom of elbow, or human paces or human heights, etc. However, it was discarded later because these methods were different for different countries and were limited to measure the long distances.

Problem 5: The Moon subtends an angle of 1° 55’ at the baseline equal to the diameter of the Earth. What is the distance of the Moon from the Earth? (Radius of the Earth is 6.4 × 10⁶ m)

Solution:

Given:

The angle subtended by moon, θ = 1° 55’ = 115’

We know, 1’ = 60’’ and 1’’ = 4.85 × 10^-6 rad

Therefore, 115’ = (115 × 60)’’ × 4.85 × 10^-6 rad = 3.34 × 10^-2 rad

The baseline for the Moon is the diameter of the Earth, b = 2 × 6.4 × 10⁶ m = 1.28 × 10⁷ m

Distance of the Moon from the Earth, x = b ⁄ θ

= 1.28 × 10⁷ m ⁄ 3.34 × 10^-2 rad

= 3.83 × 10⁸ m

Hence, the distance of the Moon from the Earth is 3.83 × 10⁸ m.
See less
0

Share
Share

Share on Facebook

Share on Twitter

Share on LinkedIn

Share on WhatsApp

Report

0

W3spoint99Begginer

Asked: January 17, 2025In: Physics

Measurement of Area, Volume and Density (Class 11 – Physics)

0

Please Explain Measurement of Area, Volume and Density (Class 11 – Physics).

Saralyn Begginer

Added an answer on January 17, 2025 at 3:25 pm

When Humans look at their childhood pictures, the first thing they realize is how tall or heavy they have become as compared to the early stages of their lives. Noticing the increment in the weight or becoming taller is done through measurement. Measurement is required everywhere in order to specifiRead more

When Humans look at their childhood pictures, the first thing they realize is how tall or heavy they have become as compared to the early stages of their lives. Noticing the increment in the weight or becoming taller is done through measurement. Measurement is required everywhere in order to specifically compare a quantity’s value from its original value. There can be many examples where measurement is required, For example, a thermometer is used to measure the temperature in Celsius of the body, the clocks on the wall are used to measure time in hours, and so on.

Measurement

Calculating the value of one quantity by comparing it with the standard value of the same physical quantity is called Measurement. It can be said that measurement associates the physical quantity with its numeric value.

Normally, objects are measured by placing them next to each other, and it can be explained which one is heavier or taller, etc. Measuring an object gives two results- value and unit of the quantity. For example, The length of the scale is 15 cm long where 15 is the value and the centimeter is the unit used for length.

Metric System

Metric system is the system that came from the decimal system and this system is used to measure basic quantities, metric system paves the way for the conversion of units, that is, the conversion of bigger units into smaller and vice-versa is possible due to the system. The basic quantities that are present are meter, gram, and liters, and they are used to measuring quantities of length, volume/mass, and capacity.

Measurement of Length

According to the metric system, length is calculated in meters. However, it can easily be converted into other forms depending upon the requirement, for instance, if the requirement is to measure the bigger quantity, it should be measured in kilometers, if the requirement is to measure something smaller, it should be in centimeters. Let’s say, the requirement is to measure a certain distance, it should either be in meters or kilometers.

Below is the easier way to explain the conversion,

Measurement of Area

In the standard way, the area of any quantity is measured in meter², since the area is a two-dimensional quantity that is scalar in nature. It involves lengths going in two different directions known as length and breadth. The area of bigger and smaller quantities can be converted easily using different units, for example, if the area of a small table is to be measured, it is measured in cm² and if the area of the plot is to be measured, the unit used is meter².

Below is the easier way to explain the conversion,

Measurement of Volume

The volume of any quantity is three-dimensional in nature, that is, the length if going in three directions, unlike length or area, the volume contains capacity. The standard unit used to measure volume is meter3. The unit is converted into bigger and smaller units like decimeter3 or kilometer3 based on how big or small the quantity is, it is done by simply dividing/ multiplying by tens, hundreds, thousands, and so on.

Below is the easier way to explain the conversion,

Measurement of Density

The density of any object is defined as the mass of that object per unit volume. Density tells how close or far away molecules are packed in a certain volume. The very famous scientist known as Archimedes discovered the concept of the Density of an object. In the metric system, Density is measured in kg/m³ and is represented as D or ρ. Therefore, it can be denoted as,

$Density (D\ or\ ρ)=\frac {Mass}{Volume}(kg/m^3)$

Note:

Density has big significance in real life. One example to prove the same is the concept of an object floating on water, The density of any object helps in identifying whether an object can float on water or not. If the density of the object is lesser than that of water (997.7 kg/m³), it will float on water.

The SI unit of density is kg/m³, but for measurement of solids, g/cm³ can also be used. In order to measure the density of liquids, mostly g/ml is used.