Please Explain Measurement of Area, Volume and Density (Class 11 – Physics).
The word science comes from a Latin verb, Scientia. All the natural phenomena in the universe are governed by a systematic understanding known as Science. Natural phenomena can be predicted, controlled, modified as well as eradicated using the concepts of Science. It can be considered to be a globalRead more
The word science comes from a Latin verb, Scientia. All the natural phenomena in the universe are governed by a systematic understanding known as Science. Natural phenomena can be predicted, controlled, modified as well as eradicated using the concepts of Science. It can be considered to be a global human endeavor. Science is concerned with physical nature and its aspects. It includes imagination, experimentation, and deduction. Knowledge about Science has been gained by humans through experiments, observations, and trials conducted on the surrounding objects. Therefore, it is both knowledge and a process. The systematic and organized knowledge collected through various sources has formed a large pool, which is so vast today that it has been divided into many branches and sub-sections :
- Physical Science- The science about the study of inanimate natural objects is referred to as the physical sciences. It majorly includes the following branches:
- Physics
- Chemistry
- Geology
- Geography etc
- Biological Science- The scientific study of life is referred to as the biological sciences.
- Botany- Concerned with the study of plants.
- Zoology- Concerned with the study of animals.
- Ornithology etc
Scientific Method and Scientific Theory
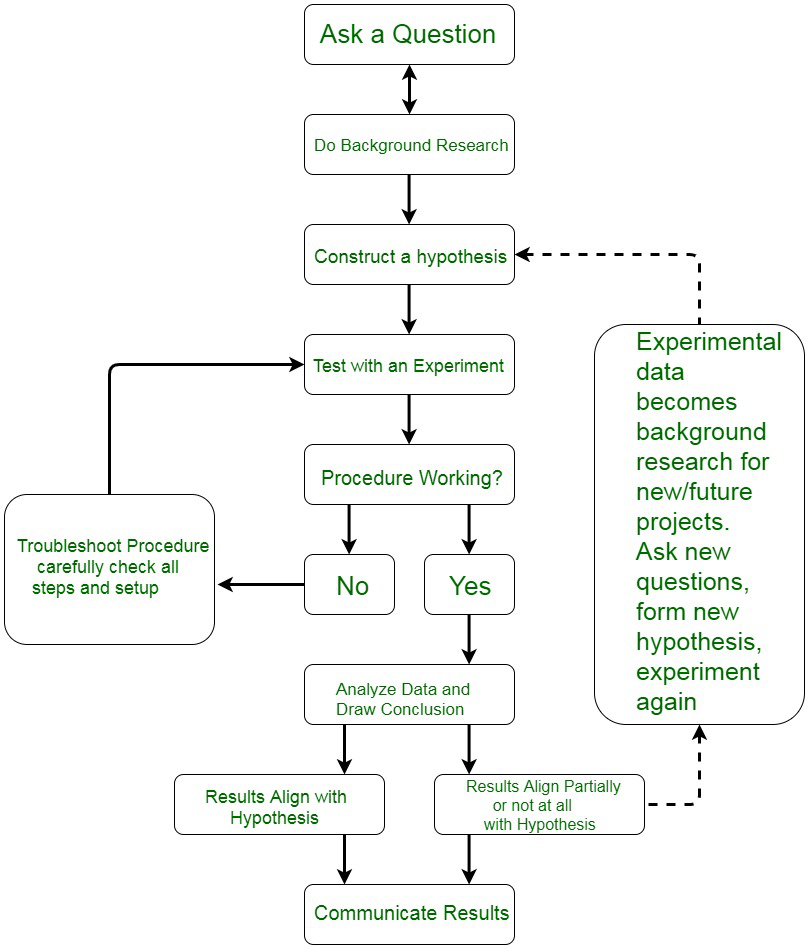
The scientific method is a way to gain knowledge in a systematic and organized way. The process in the scientific method involves creating conjectures (hypotheses), deriving predictions out of these, and then carrying out empirical observations to validate those formulated and stipulated conjectures.
The scientific method goes through the formation of a sequence of steps to reach from the knowledge pool to well-formulated derivations and formulae. It consists of the following crucial steps :
- Systematic Observations
- Controlled Experiments
- Qualitative and Quantitative reasoning
- Mathematical Modelings
- Prediction and verification of theories.
- Speculation or Prediction
Physics and its scope
Physics is the branch of science related to the study of basic laws of nature and their manifestations concerned with the different natural phenomena. It is also referred to as the “fundamental science” because it constrains all the other significant branches of the sciences. It can be considered to be the study of the physical world and matter along with its motion through space and time. It also pertains to the concepts of energy and force as well.
Physics consist of two principal types of approaches :
- Unification- Different constraints are applied to all the phenomena occurring together as a collection of universal laws in different domains in the world. It is an attempt to unify various laws and combine to carry out an activity. It is based on trial and process. For instance, both electric and magnetic phenomena are governed by electromagnetic laws.
- Reduction- This approach is based on the principle of deriving the properties of complex systems from the interactions, dependencies, and properties of their constituent parts. It can be used to understand the working of complex systems. For instance, the temperature of a system is reduced to average kinetic.
Scope of Physics
The scope of physics spreads over both massive objects like the universe and its surroundings, as well as to negligibly small-sized particles, like electrons, protons, etc., It is vast as it converts quantities with varying lengths stretching over a magnitude as high as 1060 m (study of the universe) or as low as 10-12 m (study of electrons, protons, etc). It also encompasses a wide range of masses from minutely small, like protons, neutrons etc., 10-10 kg, to highly massive galaxies, 1080 kg. Physics considers both the microscopic and macroscopic domains.
Physics is divided into two major categories based on its scope:
- Classical Physics: Deals with the macroscopic phenomena (mechanics, thermodynamics, and electromagnetism). It can be considered to be a sub-branch of applied mathematics. The laws of motion framed by Isaac Newton were designed and developed keeping in mind the principles of classical physics.
- Modern Physics: Deals with microscopic phenomena (Special Relativity, Quantum Mechanics).
Some Branch of Physics
- Mechanics- The branch of physics dealing with the movement of physical objects, more specifically the relationships between force, matter, and motion associated between them. It takes into consideration the objects both at rest and in motion.
- Electrodynamics- The branch of physics dealing with rapidly changing electric and magnetic fields. It also pertains to the understanding of the particle motion and interactions produced within the variable fields. Maxwell devised numerous laws that are concerned with the motion of electric fields and their attributes.
- Optics- The branch of physics dealing with the behavior and the interactions of light with each other. It can be used to simulate the construction of devices used to visualize and detect the aspects and components of light. It takes into account both ray and wave optics. It involves concepts related to the formation of images and the working of topics of reflection, refraction as well as diffraction.
- Thermodynamics- The branch of physics related to heat and energy and its involved concepts. It also described the relationship with radiation along with the physical properties of matter. It also includes the conversion of heat into different types of energy; mechanical or electrical energy.
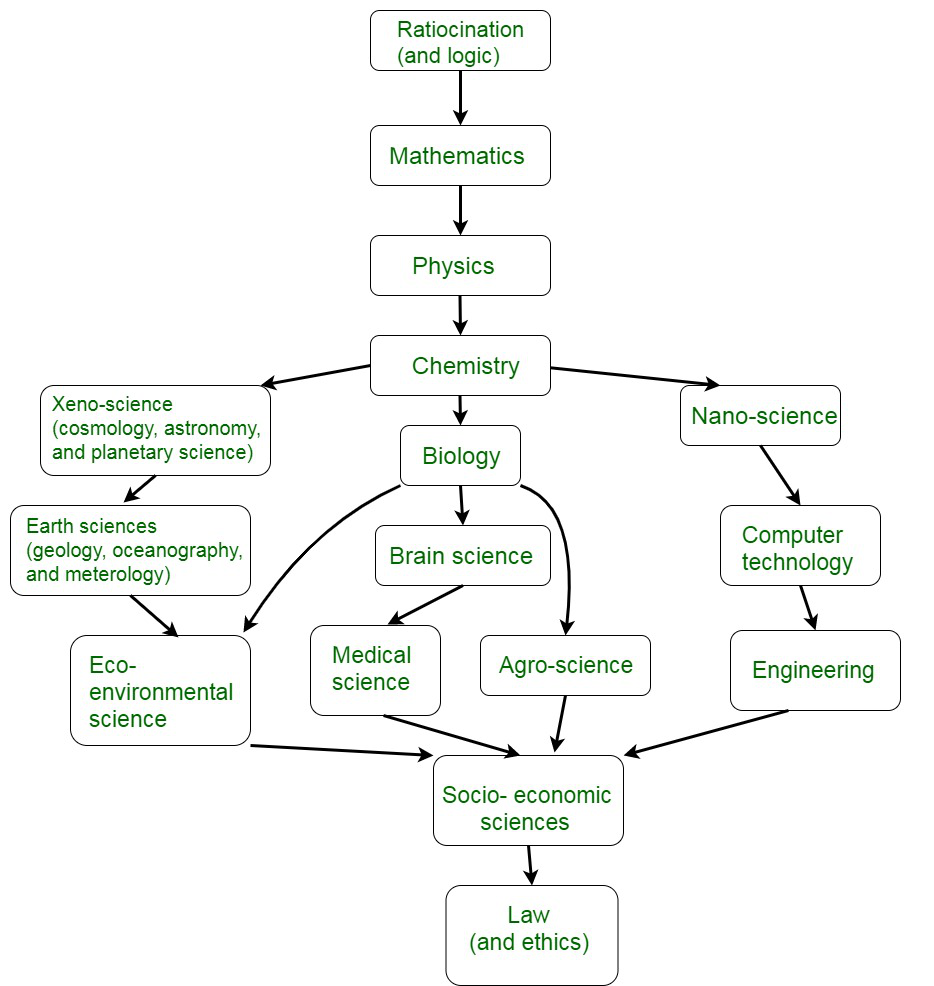
Physics in Relation to Other Sciences
Physics is a very significant branch of science that plays a crucial role in understanding the developments pertaining to the other branches of science, such as Chemistry, Biology, etc.
- Physics in relation to Mathematics. The study of physical variables involved in the study of mathematics has led to the discovery of ideas of differentiation, integration, and differential equations involved in the estimation of quantities. Theories in physics and derivations in mathematics coexist with each other. Math is considered to be a deterministic tool for the development of modern theoretical physics. It provides a way to formulate and evaluate experimental results.
| Mathematics | Physics | |
| Graph | Represents a single object. | Represents a relationship between two quantities. |
| Axes | Dimensionless numbers are represented by linear scaling | Values of quantities are expressed in some units. Scaling may be linear or non-linear. |
| Origin | (0,0) | Any arbitrary position. |
| Plot range | infinite | The ranges of the quantities. |
| Slope Gradient | Dimensionless numbers have a geometric interpretation only. | Change of one quantity with respect to another. |
- Physics in relation to Biology. Physics form the essence of the field of biology. The concepts and illustrations of space, time, and matter have induced a better understanding of the existence of living organisms and the study of the laws of conversation of energy. Many diseases and ailments have been better diagnosed over the years due to developments in physics and vice versa. Disease diagnosis has been very efficient due to X-ray invention and practices.
- Physics in relation to Chemistry. Chemistry is basically an extension of Physics. The concepts associated with X-ray diffraction and radioactivity have revolutionized the study of the periodic table. The intra-particle forces, as well as internal interactions, can also be used to get a better insight into the bonding and the chemical structure of substances. The structure, behavior, and properties of matter are both easily understood with both the branches existing together.
- Physics in relation to Meteorology. Meteorology holds an explicit part in the discipline of physics. It tends to explain nature’s observed behavior through estimated hypotheses and conjectures while taking into consideration the various relativistic repercussions. Atmospheric physics and meteorology use both mathematical and physical models to understand the weather and climatic conditions. It also relates to the descriptive mathematical and computer modeling of atmospheric dynamics.
- Physics in relation to Astronomy. The branch of astronomy is considered to be applied physics since it applies the scientific hypotheses and basic rules of physics to further the understanding of the celestial bodies and universe.For instance, the discovery and usage of radio telescopes, as well as optical telescopes, have stipulated an easy way to explore the universe.
| Type of forces | Governs |
| Gravitational force | All objects in the universe |
| Weak nuclear force | Particularly electrons and neutrinos. |
| Electromagnetic force | Charged particles |
| Strong nuclear force | Nucleons, heavier elementary particles |
The other sciences, like geology, oceanology, seismology, etc, also use some laws of physics.
Sample Problems
Problem 1: What is “high-energy” physics?
Solution:
High-energy physics, which is also termed particle physics, refers to the study of the elementary constituents of matter and energy along with their corresponding interactions. Particle physics is concerned with the design and development of high-energy accelerators and detectors.
Problem 2: Explain the relation of physics to seismology.
Solution:
Seismology is also referred to as the scientific study concerned with earthquakes and their related phenomena, such as volcanic eruptions. The movement of the earth’s crust, that is, the tectonic shifts and the types of waves emitting energy helps us in studying the earthquake and its repercussions.
Problem 3: Differentiate between weak and strong nuclear forces.
Solution:
The difference between weak and strong nuclear forces are as follows:
Weak nuclear forces Strong nuclear forces It makes the radioactive particles decay. It keeps the protons and neutrons of a nucleus together. Weak and very short-ranged. Strong and short ranged. Example: Conversion of a proton to a neutron. Example: fusion process between stars and the sun.
Problem 4: What is the difference between classical and modern physics?
Solution:
Classical physics deals with the study of objects on a macroscopic scale, which can be studied with the largely unaided five human senses. This is in comparison to modern physics, which is concerned with the nature and behavior of particles and energy at the sub-microscopic level. The laws of one branch of physics remain inapplicable to the other branch and vice versa. Also, most of the laws of classical physics are deterministic.
Problem 5: Define astrophysics.
Solution:
Astrophysics is a branch of science dealing with the methods and principles deployed in the study of astronomical objects and phenomena of the universe.
Problem 6: Explain the reasons behind the durability of scientific knowledge.
Solution:
- It is easily corroborated by multiple scientists working independently.
- Consistent and accurate with different scientists.
- Vast knowledge accumulating over many years.
Problem 7: Is it possible to modify a scientific theory?
Solution:
See lessA scientific theory can be revised if required to accommodate new phenomena or data. It is not fixed and can be reformulated.


When Humans look at their childhood pictures, the first thing they realize is how tall or heavy they have become as compared to the early stages of their lives. Noticing the increment in the weight or becoming taller is done through measurement. Measurement is required everywhere in order to specifiRead more
When Humans look at their childhood pictures, the first thing they realize is how tall or heavy they have become as compared to the early stages of their lives. Noticing the increment in the weight or becoming taller is done through measurement. Measurement is required everywhere in order to specifically compare a quantity’s value from its original value. There can be many examples where measurement is required, For example, a thermometer is used to measure the temperature in Celsius of the body, the clocks on the wall are used to measure time in hours, and so on.
Measurement
Calculating the value of one quantity by comparing it with the standard value of the same physical quantity is called Measurement. It can be said that measurement associates the physical quantity with its numeric value.
Normally, objects are measured by placing them next to each other, and it can be explained which one is heavier or taller, etc. Measuring an object gives two results- value and unit of the quantity. For example, The length of the scale is 15 cm long where 15 is the value and the centimeter is the unit used for length.
Metric System
Metric system is the system that came from the decimal system and this system is used to measure basic quantities, metric system paves the way for the conversion of units, that is, the conversion of bigger units into smaller and vice-versa is possible due to the system. The basic quantities that are present are meter, gram, and liters, and they are used to measuring quantities of length, volume/mass, and capacity.
Measurement of Length
According to the metric system, length is calculated in meters. However, it can easily be converted into other forms depending upon the requirement, for instance, if the requirement is to measure the bigger quantity, it should be measured in kilometers, if the requirement is to measure something smaller, it should be in centimeters. Let’s say, the requirement is to measure a certain distance, it should either be in meters or kilometers.
Below is the easier way to explain the conversion,
Measurement of Area
In the standard way, the area of any quantity is measured in meter2, since the area is a two-dimensional quantity that is scalar in nature. It involves lengths going in two different directions known as length and breadth. The area of bigger and smaller quantities can be converted easily using different units, for example, if the area of a small table is to be measured, it is measured in cm2 and if the area of the plot is to be measured, the unit used is meter2.
Below is the easier way to explain the conversion,
Measurement of Volume
The volume of any quantity is three-dimensional in nature, that is, the length if going in three directions, unlike length or area, the volume contains capacity. The standard unit used to measure volume is meter3. The unit is converted into bigger and smaller units like decimeter3 or kilometer3 based on how big or small the quantity is, it is done by simply dividing/ multiplying by tens, hundreds, thousands, and so on.
Below is the easier way to explain the conversion,
Measurement of Density
The density of any object is defined as the mass of that object per unit volume. Density tells how close or far away molecules are packed in a certain volume. The very famous scientist known as Archimedes discovered the concept of the Density of an object. In the metric system, Density is measured in kg/m3 and is represented as D or ρ. Therefore, it can be denoted as,
Sample Problems
Question 1: Convert the following: m3 to mm3, liter to meter3, mile3 to km3.
Solution:
Question 2: What is the difference between the metric system and the imperial system of measurement?
Answer:
Question 3: Calculate the density of an object having a mass of 1200kg and its volume is 10m3.
Solution:
Question 4: There are two large boxes filled with biscuits. The first has 10 biscuits and the second has 20 biscuit packets present in it. The box have the same volume. Explain which box will weigh more?
Answer:
Question 5: A cube is given which has a volume of 1000m3. Calculate the surface area of the cube in cm3.
Solution:
Question 6: The length and the breadth of a cuboid are same, but the height is twice in value. If the volume of the cuboid is 54000m3, find the length, breadth and height of the cuboid in centimeters.
Solution:
Question 7: A cm scale has a limit of 15 points, how long is the scale in meters?
Solution:
See less