Home/physics

StackOverflow Latest Questions

W3spoint99
  • 0
W3spoint99Begginer
Asked: January 17, 2025In:
  • 0

Please Explain Length Measurement (Class 11 – Physics).

class 11length measurementphysicsscience
  1. Saralyn
    Saralyn Begginer

    Previously, length was measured using units such as the length of a foot, the breadth of a palm, and so on. The ‘Cubit’ was one of the first means of measuring length. It is the length of the arm from the elbow to the tip of the fingers. These units vary from person to person, resulting in non-unifoRead more

    Previously, length was measured using units such as the length of a foot, the breadth of a palm, and so on. The ‘Cubit’ was one of the first means of measuring length. It is the length of the arm from the elbow to the tip of the fingers. These units vary from person to person, resulting in non-uniform measures.

    How can we know how far the moon is from the earth or how far the moon is from the sun? How did we determine the earth’s diameter? Measuring length isn’t always simple or easy. We’ll try to respond to these queries in the sections below. In addition, we will learn about the many methods for measuring length.

    Length

    The measurement or amount of anything from one end to other is referred to as length.

    In other terms, it is the largest of the two or the highest of three geometrical form or item dimensions. The width and length of a rectangle, for instance, are its dimensions. Furthermore, under the International System of Quantities, length is a quantity with the dimension distance.

    The meter, abbreviated as m, is the basic unit for length in the International System of Units (SI). The length or distance is measured in kilometers (km), meters (m), decimeters (dm), centimeters (cm), and millimeters (mm) in the metric system (mm). It is possible to convert quantities from meters to centimeters, kilometers to meters, centimeters to millimeters, and so on.

    Measurement of Length

    There were no modes of transportation available in ancient times. People used to travel on foot or by using animals to transport goods. Over time, the term “wheel” was coined. This signified a significant shift in human forms of transportation. Since then, new forms of transportation have been invented and improved regularly. The steam engine was created, and it had a great influence and was instrumental in shaping the world as we know it today.

    As a result, transportation has a lengthy history. Did the folks have any idea how far they had to go? To go to any location, one must first determine how far away it is. This aids in deciding whether to walk, take the train, bus, or fly to that location. To determine how far apart two locations are, we must first determine the distance between them. But what exactly does measurement imply? What is the best way to measure a physical quantity? The comparing of an unknown amount to a known amount is known as measurement. A numerical number known as “magnitude” and a “unit” are used to indicate the outcome of the measurement. A ‘unit’ is a pre-determined unit of comparison against which other physical quantities are measured.

    The length of the foot, the breadth of the palm, and other such quantities were used to measure the length in the past. The ‘Cubit’ was one of the first means of measuring length. It is the length of an arm measured from elbow to tips of fingers. These units varied from person to person, resulting in non-uniform measures. A set of standard units of measurement has been recognised all around the world to preserve uniformity in measurements.

    The International System of Units (SI) is one of the most widely used measurement systems in the world. The basic unit of length in the SI system is the meter. The C.G.S. system is another system of units in which the centimeter is the basic unit of length.

    Conventional Methods of Measurements

    Historically, the human body served as the foundation for length units.

    • Inch: An inch is a unit of measurement that was once used to measure the length of little things such as the length of paper, the seam of cloth, and so on.
    • Foot: A foot is a unit of length that is commonly defined as 15.3 per cent of a human body’s height, with an average height of 160 cm. This unit differed from one location to the next and from one transaction to the next. The Romans and Greeks favored this unit, which was commonly used to compute the height of humans and livestock, the size of a piece of fabric, the size of a structure, and so on.
    • Cubit: A cubit is a unit of length based on the length of the forearm, which is commonly measured from the tip of the middle finger to the forearm’s length bottom of the elbow. The Egyptians and Mesopotamians favored this unit. Cubit rods have been unearthed among the ancient Egyptian civilization’s relics. These rods are typically 20 inches long and are split into seven palms, each of which is split into four fingers, which are further subdivided.
    • Yard: A yard is a measurement of distance based on human paces. It is usually measured in two cubits, which is around 36 inches.
    • Mile: A mile is equal to 1,000 paces, where a pace is equal to two steps and the walker returns to the same foot.

    A foot is 12 inches long, and a yard is three feet long. It was simple to describe how distant the next village was and to determine if an object would fit through a doorway using these dimensions. These dimensions also made it easier for individuals to swap garments and wood.

    Scale

    Triangulation Method

    Let’s take a closer look at what the triangulation approach entails. How might triangulation assist us in determining the distances between distant stars? The parallax approach makes use of the fact that a triangle may be entirely defined using only three parts. Triangulation is the process of determining the values of a triangle to determine an item’s position. Surveyors and architects frequently employ such techniques.

    Triangulation is the method of identifying the location of a point by calculating the angles to it from two known sites rather than calculating distances directly.

    Triangulation Example

    Let’s put this into practice with a real-life scenario. How can we estimate a large object distance from any distance without actually measuring it? It may be measured using the triangulation method.

    Triangulation Method of measurement

    • Let’s start by constructing a fixed baseline with two points AB.
    • The angle formed by point A concerning the object is denoted by α, whereas the angle formed by point B concerning the object is marked by β.
    • Now that we have the baseline AB and the angles, we can determine the remainder of the triangle’s attributes, such as the position of the third point, which is the object.

    Parallax Method

    The displacement or shift in the apparent location of an item when observed from two distinct points of view is known as parallax.

    The two places of vision each have their own line of sight, and parallax is defined as half the angle between them. When you’re driving in a car and glance about, you’ll notice that items far away appear to move more slowly than items closer to you. This is the parallax effect. Because the parallax of nearby objects is greater than that of distant ones, the parallax may be utilised to measure distances.

    When the phenomena of parallax is coupled with triangulation, the position of the item may be determined with great precision. The parallax method is commonly used by astronomers to determine the distances between stars.

    Distance Measurement by Parallax Method

    The principle of triangulation is used to the measuring of distance through parallax. We learned from triangulation that a triangle may be completely specified if two angles and sides are known.

    The distance of a faraway star is being computed in the image below. The star closer to Earth than the farthest one gives the limited parallax value. By observing the star from two known places on Earth that form the triangle’s baseline, we may determine the value of the parallax angle.

    Parallax Method

    Let’s denote the parallax half-angle between two places on Earth ‘p.’ The radius of the Earth is the greatest value of ‘d,’ and the distance of the star may be considered to be just slightly more than that of the sun. Because the distance from the sun is several orders of magnitude lower than the radius of the Earth, the parallax angle we obtain is exceedingly modest.

    Application

    The distance to an object measured in parsecs (in terms of light speed) is equal to the reciprocal of parallax angle measured in arcseconds.

    Relation between the distance of a star, and its parallax is given as:

    D = 1 ⁄ p

    where D is the distance of star and p is the parallax angle.

    To solve the difficulty of tiny ratios, the parallax of a star is most commonly estimated using yearly parallax, which is defined as the difference in a star’s location as seen from the Earth and the Sun. Instead of using the Earth’s radius as a fixed baseline, the radius of the Earth’s revolution around the Sun is used, which increases the size of the baseline and hence the top angle, making it simpler to measure.

    However, for any celestial objects near to the Earth, we can consider the diameter of the Earth as a baseline, and the distance of any celestial objects is given as:

    x = b ⁄ θ

    where x is the distance of the object from the Earth, b is the baseline or diameter of the Earth and θ is the angle subtended by the object.

    Sample Problems

    Problem 1: If a person covers 1.5 yards in one step, how much distance will he cover in 30 steps?

    Solution:

    Given:

    Total number of steps, n = 30

    Value of 1 step, d = 1.5 yards

    Total distance covered by the person, D = n d

    = 30 × 1.5 yard

    = 45 yards

    Hence, the distance covered by the person is 45 yards.

    Problem 2: Astronomers apply which method to determine how far away a star is?

    Answer:

    Astronomers use parallax to calculate the distance between stars. Trigonometric parallax is another name for parallax.

    Problem 3: What is parallax?

    Answer:

    The two items appear to be coincident when seen in a straight line. There is a relative displacement between the things if they are at separate locations and the eye is shifted sideways. The closer item travels in the opposite direction from the eye, whereas the further object travels in the same direction.

    When two things are perceived in a straight line and the eye is shifted to the side, this is referred to as parallax.

    Problem 4: What was the conventional method of measuring the length?

    Answer:

    The length was measured in history with the help of human body. These were based on the several methods like distance from tip of middle finger to bottom of elbow, or human paces or human heights, etc. However, it was discarded later because these methods were different for different countries and were limited to measure the long distances.

    Problem 5: The Moon subtends an angle of 1° 55’ at the baseline equal to the diameter of the Earth. What is the distance of the Moon from the Earth? (Radius of the Earth is 6.4 × 106 m)

    Solution:

    Given:

    The angle subtended by moon, θ = 1° 55’ = 115’

    We know, 1’ = 60’’ and 1’’ = 4.85 × 10-6 rad

    Therefore, 115’ = (115 × 60)’’ × 4.85 × 10-6 rad = 3.34 × 10-2 rad

    The baseline for the Moon is the diameter of the Earth, b = 2 × 6.4 × 106 m = 1.28 × 107 m

    Distance of the Moon from the Earth, x = b ⁄ θ

    = 1.28 × 107 m ⁄ 3.34 × 10-2 rad

    = 3.83 × 108 m

    Hence, the distance of the Moon from the Earth is 3.83 × 108 m.

    See less
W3spoint99
  • 0
W3spoint99Begginer
Asked: January 17, 2025In:
  • 0

Please Explain System of Units (Class 11 – Physics).

class 11physicssciencesystem of units
  1. Saralyn
    Saralyn Begginer

    Measurement forms the fundamental principle to various other branches of science, that is, construction and engineering services. Measurement is defined as the action of associating numerical with their possible physical quantities and phenomena. Measurements find a role in everyday activities to aRead more

    Measurement forms the fundamental principle to various other branches of science, that is, construction and engineering services. Measurement is defined as the action of associating numerical with their possible physical quantities and phenomena. Measurements find a role in everyday activities to a large extent. Therefore, it is necessary to study and explore the associated elements along with their theoretical foundations, conditions as well as limitations. It defines the units to be chosen for the measurement of various commodities. It also caters to the comparison of plausible units with the ones already existing of a similar kind.

    Measurement defined the new standards as well as form transductions for the quantities which do not have any possible access for direct comparison. These physical quantities can be converted into analogous measurement signals.

    Measurements may be made by unaided human senses, generally termed as estimates. It can also be estimated by the use of instruments, which may range in complexity from simple rules for measuring lengths to highly complex analogous systems to handle and design the commodities beyond the capabilities of the senses. Thus, the measurements may range from buying some quantity of milk (in L) or to the highly complex mechanisms, such as radio waves from a distant star or the nuclear bomb radiations. Therefore, we can consider that a measurement, always involves a transfer of energy or interaction between the object and the observer or observing instrument.

    Measurement of Height of a person

    Unit

    The unit of a specified physical quantity can be considered as an arbitrarily chosen standard that can be used to estimate the quantities belonging to similar measurements. The units are well accepted and recognized by the people and well within all guidelines.

    A physical quantity is measured in terms of the chosen standards of measurement.

    The chosen standard is recognized as the unit of that corresponding physical quantity. A standard unit, in short, is a definite amount of a physical quantity. These standard units can be quickly reproduced to create a wide variety of units and are internationally accepted and accessible.

    The measurement of any physical quantity is based on a formula, nu,

    where, n = numerical value of the measure of the quantity,

    u = unit of the quantity.

    Standard

    The actual physical embodiment of the unit of a physical quantity is termed as a standard of that physical quantity. The standard is expressed in terms of the numerical value (n) and the unit (μ).

    Measurement of physical quantity = Numerical value × Unit

    For example: Length of a rod = 12 m. Here 12 is its numerical segment and m (meter) is the unit.

    Fundamental Units

    Fundamental units are elementary in nature, that is, they can be expressed independently without any dependence on any other physical quantity. This implies that it is not possible to resolve it further in terms of any other physical quantity. It is also termed as a basic physical quantity. Fundamental quantities have their own values and units.

    Fundamental Quantities Fundamental Units Symbol
    Length meter m
    Mass kilogram kg
    Time second s
    Temperature kelvin k
    Electric current ampere A
    Luminous intensity candela cd
    Amount of substance mole mol

    Supplementary Fundamental Units

    There are two other supplementary fundamental units, namely Radian and steradian are two supplementary which measures plane angle and solid angle respectively.

    Supplementary Fundamental Quantities Supplementary Unit
    Plane angle radian
    Solid angle steradian
    • Radian (rad)
      One radian is equivalent to an angle subtended at the center of a circle by an arc of length equal to the radius of the circle. It is the unit represented for the plane angle.

    θ = 1 radian

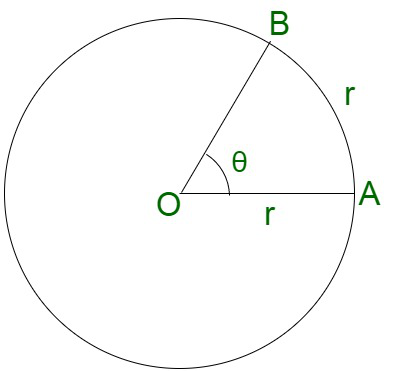
    dθ=\left(\frac{ds}{r}\right)\ radian

    • Steradian (sr)
      One steradian is equivalent to the solid angle subtended at the center of a sphere by its surface. Its area is equivalent to the square of the radius of the sphere.It is the unit represented for the solid angle. Solid angle in steradian,

    Ω = 1 steradian

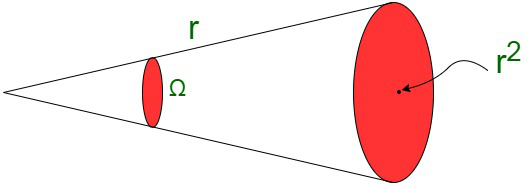
    dΩ =\frac{Area\ cut\ out\ from\ the\ surface\ of\ sphere}{(Radius)^2}\\ dΩ =\left(\frac{dA}{r^2}\right)\ steradian

    Properties of Fundamental Units

    Any standard unit should have the following two properties:

    • Invariability
      The standard unit must be invariable. Thus, defining distance between the tip of the middle finger and the elbow as a unit of length is not invariable.
    • Availability
      The standard unit should be easily made available for comparing with other quantities.

    The seven fundamental units of S.I. have been defined as under.

    • Meter (m)
      Defined as 1650763.73 times the wavelength, in vacuum of the orange light emitted in transition from 2p10­  to 5d5.
    • Kilogram (kg) 
      Defined as the mass of a platinum-iridium cylinder kept at Serves.
    • Second (s) 
      Time taken by 9192631770 cycles of the radiation from the hyperfine transition in cesium – 133 when unperturbed by external fields.
    • Ampere (A)
      The constant current which, if maintained in each of two infinitely long, straight, parallel wires of negligible cross-section placed 1 m apart, in vacuum, produces between the wires a force of 2×10-7 newton per meter length of the wires.
    • Kelvin (K)
      Temperature is measured with absolute zero as the zero and the triple point of water as the upper fixed point on the thermodynamic scale. The interval is divided into 273.15 divisions and each division is considered to be unit temperature.
    • Candela (cd)
      The luminous intensity in the perpendicular direction of a surface of \frac{1}{600000} square meter of a full radiator at the temperature of freezing platinum under a pressure of 101325 newtons per square meter.
    • Mole (mol)
      The mole is the amount of any substance which contains as many elementary entities as there are atoms in 0.012 kg of the carbon isotope \frac{12}{6} C.

    Derived units

    The derived units are in usage for the commodities where the units are obtained from a combination of fundamental units. Derived units are sometimes assigned names. For instance, the S.I unit of force is kg ms-2 , termed as Newton (N). The unit of power is kg m2 s-3 , termed as watt (W).

    Steps to find Derived Units

    • Fetch the formula for the quantity whose unit is to be derived.
    • Substitute units of all the involved quantities. The chosen units should all belong to one system on units in their fundamental or standard form.
    • Simplify for the derived unit of the quantity to compute its final unit.

    Example: Compute the unit of velocity.

    Since, we know velocity is a derived quantity, obtained from distance and time(fundamental quantities).

    Mathematically ,

    velocity =  displacement/time

    S.I. unit of velocity = \frac{S.I.\ unit\ of\ displacement}{ S.I.\ unit\ of\ time}  = m/s

    Thus S.I. unit of velocity is m/s.

    Some Important derived units

    Some of the derived units have been given specific names, depending on the increase in their usage , though they are not recognized in S.I units.

    • Micron (mm) = 10-6 m
    • Angstrom (Å)  = 10-10 m
    • Fermi (fm) = 10-15 m
    • Barn (b) = 10-28 m2

    Systems of Units

    Any system of units contains the entire set of both fundamental as well as derived units, for all kinds of physical quantities. The preferred system of units are the following :

    • CGS System  (Centimeter Gram Second)
      The unit of length is centimeter, the unit of mass is gram and the unit of time is second according to the guidelines of this system.
    • FPS System  (Foot Pound Second)
      The unit of length is foot, the unit of mass is pound and the unit of time is second according to the guidelines of this system.
    • MKS System (Meter Kilogram Second)
      The unit of length is meter, the unit of mass is kilogram and the unit of time is second according to the guidelines of this system.
    • SI System 
      The System Internationale d’ Units, that is S.I system contains seven fundamental units and two supplementary fundamental units.

    Note:

    While computation of values for any physical quantity, the units for the involved derived quantities are treated as algebraic quantities till the desired units are obtained.

    Advantages of S.I Unit System

    The S.I unit of measurement is preferred over other units of measurement, because,

    • It is internationally accepted.
    • It is a metric system.
    • It is a rational and coherent unit system,
    • Easy conversion between CGS and MKS systems of units.
    • Uses decimal system, which is easy to understand and apply.

    Other Important Units of Length

    The distances can be infinitely larger in magnitude, which cannot be depicted in terms of meters or kilometers. For instance, the distances of planets and stars etc. Therefore, it is necessary to use some larger units of length such as ‘astronomical unit’, ‘light year’, parsec’ etc. while making such calculations, some of which are :

    • Astronomical Unit – The average separation between the Earth and the sun.
      1 AU = 1.496 x 1011 m.
    • Light Year – The distance travelled by light in vacuum in one year.
      1 light year = 9.46 x 1015 m.
    • Parsec – The distance at which an arc of length of one astronomical unit subtends an angle of one second at a point.
      1 parsec = 3.08 x 1016 m
    • Fermi – Size of a nucleus is expressed in ‘fermi’.
      1 fermi = If = 10-15 m
    • Angstrom – Size of a tiny atom
      1 angstrom = 1A = 10-10 m

    Sample Problems

    Problem 1. Convert the unit of G, which is gravitational constant, G = 6.67 x 10-11Nm2/kg2 in CGS system.

    Solution: 

    Since, we have

    G = 6.67 x 10-11 Nm2/kg2

    Converting kg into grams, 1 kg = 1000 gms

    = 6.67 x 10-11 x 108 x 103 cm3/g1 s2

    = 6.67 x 108  cm3/g1 s2

    Problem 2. Name the S.I units of the following commodities : 

    a. Pressure

    b. Solid angle

    c. Luminous intensity.

    Solution: 

    a. Pascal

    b. Steradian

    c. Candela

    Problem 3. Derive the S.I unit of latent heat. 

    Solution: 

    Latent heat = \frac{Heat energy}{Mass}

    Latent\space Heat = \frac{Q}{m} \\ =\frac{ kg m^2 s^{-2}}{kg} \\ = m^2 s^{-2}

    Problem 4: How are A0 and A.U related? 

    Solution: 

    Describing both quantities in terms of meters,

    Ao = 10-10m

    and 1 A.U. = 1.4961011m.

    Therefore,

    1 A.U. =  1.496 x 1011 x 1010 A0

    1 A.U = 1.496 x 1021 A0

    Problem 5: Describe 1 light-year in meters. 

    Solution: 

    A light-year is a distance travelled by light in 1 year with the speed of light :

    = 9.46 x 1011 m

    See less
W3spoint99
  • 0
W3spoint99Begginer
Asked: December 30, 2024In:
  • 0

Explain Fundamental Forces in Nature (Class 11 – Physics) – Notes

cbseclass 11forcesfundamentalnaturephysics
  1. Saralyn
    Saralyn Begginer

    Fundamental Forces The most beautiful phenomenon that can be seen in physics is that how universe is so disciplined and synced together. The force has kept the universe bind together. Forces have always played an important role in the human existence, but it is not realized by humans. Human beings cRead more

    Fundamental Forces

    The most beautiful phenomenon that can be seen in physics is that how universe is so disciplined and synced together. The force has kept the universe bind together. Forces have always played an important role in the human existence, but it is not realized by humans. Human beings constantly experience some force acting on them like gravitational force, etc.  There are some forces that naturally exist in the universe, they are known as Fundamental Forces. Let’s learn about them in some detail.

    Force

    Force is an interaction, either with contact or without contact. When there is no opposition given to the Force, It can result in changing the motion, shape, position, of a body. Whenever some interaction occurs between two objects, there is a certain force acting upon them. There are many types of Forces present, For instance, Applied Force, Gravitational Force, Frictional Force, Tension Force, etc.

    Fundamental Forces in nature

    These forces are so well-defined that they cover the macroscopic and microscopic forces present in nature. The forces learned or seen by humans in everyday life, from frictional force, pull, push, thrust, etc. are known as derived forces, and they are not considered the fundamental forces. The derived forces are actually derived from the fundamental forces in some way or the other. Some Fundamental Forces are,

    • Gravitational Force
    • Electromagnetic Force
    • Strong Nuclear Force
    • Weak Nuclear Force

    These above-mentioned forces are responsible for all the observations obtained in forces present in the nature.

    Gravitational Force

    This force exists by the virtue of the masses of any objects. Gravitational force is the mutual force of attraction between two masses. Attraction between any mass and Earth is called Gravity. Isaac Newton first gave the concept of gravity. Gravity is the most intuitive and the weakest force present in nature. The Irony is that Gravity actually holds the planet, Solar system, Entire Universe together, yet it is known to be the weakest force present in nature.

    The Force of Gravitation is given as,

    Formula for Gravitational Force,

    F1=F2=G\frac{M1.M2}{r^2}

    Where, F = Force of Gravitation

    M1, M2 = Masses 1 and 2

    r = Distance between the masses

    G = Gravitational Constant (6.67× 10-11m3kg-1s-2)

    Electromagnetic Force

    Charges when they are at rest exert a force at each other known as the Electric force of attraction/repulsion. Like charges repel each other while unlike charges attract each other. When charges start to move and become dynamic, they develop magnetic field lines around and have magnetic force, these two forces combined are known as Electromagnetic forces present in nature.

    Magnetic force produced by current (moving charge)

    Combining the above two forces which are always perpendicular to each other will give rise to Electromagnetic Force. The force is produced by massless bosons and photons present in the charges, Electromagnetic force exists in nature and is responsible for many derived forces we experience every day, for example, Friction Force, Normal Force, Elasticity, and so on.

    Strong Nuclear Force

    It is the force of attraction between Protons and Neutrons. The force is the same whether protons and protons are present or neutrons and neutrons are present or protons and neutrons are looked at. In short, a Strong nuclear force exists between all nucleons. In short Ranges, this Force is the strongest among all the forces. It is important to note that at a distance of 10-13 cm, this force vanishes.

    Weak Nuclear Force 

    This Force is seen In the β Decay of a nucleus. Scientist named Wolfgang Pauli First predicted a particle named Neutrino. The Neutrino is an uncharged Particle that is released along with the electron in the β Decay process. During β Decay, when Beta Particle is ejected from an Atom, it tends to accelerate away from the atom and some force is required to accelerate the particle known as Weak Nuclear Force. Weak Nuclear Force is stronger than gravitational force but weaker than a strong nuclear force. 

    Table to represent Range and Relative Strength of Different Forces:

    Forces Range Relative strength
    Gravitational Force ∞ 10-38
    Electromagnetic Force ∞ 10-2
    Strong nuclear force < 10-15m 1
    Weak nuclear Force < 10-18m 10-13

    Conceptual Questions

    Question 1: Which Fundamental Force is the strongest and weakest among the fundamental forces present in nature?

    Answer:

    The strongest force present in nature is the Strong Nuclear Force and the weakest force present in nature at atomic scale is Gravity.

    Question 2: Which of the following forces are Fundamental, and which are derived in nature?

    Weak Nuclear Force, Friction Force, Gravity, Elasticity, Electromagnetic Force, Push

    Answer:

    Fundamental Forces ⇢ Weak Nuclear Force, Gravity, Electromagnetic Force.

    Derived Force ⇢ Friction Force, Elasticity, Push.

    Question 3: A statement is being used now “Gravity is not a force” Throw light on this statement.

    Answer:

    Isaac Newton initially discovered Gravity and Gravitational Force. It was then stated that gravity is a Force. Later on, with the help of Theory of Relativity, Einstein stated that Gravity is actually not a force but a result of space-time orientation. It is a consequence of masses moving along a geodesic lines in space time.

    Question 4: If the masses of 2 objects are doubled and the space between them is also doubled. How will the gravitational Force between them change?

    Answer:

    Gravitational Force is given as,

    F_G=G\frac{M_1.M_2}{r^2}

    When, Mass 1 and Mass 2 is doubled, M1’=2M1, M2’=2M2

    Distance between the masses is doubled, r’= 2r

    New Gravitational Force Between them,

    F_G'=G\frac{M_1'.M_2'}{r'^2}=G\frac{2M_1.2M_2}{4r^2} \\=G\frac{M_1.M_2}{r^2}=F_G

    Hence, The new value of gravitational Force will be same as the old Gravitational Force.

    Question 5: What are Pseudo Forces? Give Examples.

    Answer:

    Pseudo Forces are also known as Inertial Force or Fictitious Force. These forces actually do not exist and are the apparent forces that are seen due to fact that they are defined from a non-inertial frame.

    Example: A man sees another man going in a car and realized that some force is acting on the man in the car. This type of force seen is real as it is seen from a non-accelerated or inertial frame. However, the man in the car if looks at the man standing would feel that some force is acted upon the man and he is going backwards, this force is pseudo force, Since this force is seen from a non-inertial frame or an accelerated frame.

    Question 6: Which two forces have infinite range?

    Answer:

    The two fundamental forces having infinite range are Gravitational force and Electromagnetic force.

    See less
W3spoint99
  • 0
W3spoint99Begginer
Asked: December 28, 2024In:
  • 0

How is Physics related to Other Sciences?

how physics relates to other sciencesinterdisciplinary sciencephysicsphysics and astronomyphysics and astronomy relationphysics and biologyphysics and chemistryphysics applicationsphysics explainedphysics in geologyrole of physics in sciencesscience connectionsscience educationscience videoSTEM education
  1. Saralyn
    Saralyn Begginer

    The word science comes from a Latin verb, Scientia. All the natural phenomena in the universe are governed by a systematic understanding known as Science. Natural phenomena can be predicted, controlled, modified as well as eradicated using the concepts of Science. It can be considered to be a globalRead more

    The word science comes from a Latin verb, Scientia. All the natural phenomena in the universe are governed by a systematic understanding known as Science. Natural phenomena can be predicted, controlled, modified as well as eradicated using the concepts of Science. It can be considered to be a global human endeavor. Science is concerned with physical nature and its aspects. It includes imagination, experimentation, and deduction.  Knowledge about Science has been gained by humans through experiments, observations, and trials conducted on the surrounding objects. Therefore, it is both knowledge and a process. The systematic and organized knowledge collected through various sources has formed a large pool, which is so vast today that it has been divided into many branches and sub-sections :

    • Physical Science- The science about the study of inanimate natural objects is referred to as the physical sciences. It majorly includes the following branches:   
      • Physics
      • Chemistry
      • Geology
      • Geography etc
    • Biological Science- The scientific study of life is referred to as the biological sciences.
      • Botany- Concerned with the study of plants.
      • Zoology- Concerned with the study of animals.
      • Ornithology etc

    Scientific Method and Scientific Theory

    The scientific method is a way to gain knowledge in a systematic and organized way. The process in the scientific method involves creating conjectures (hypotheses), deriving predictions out of these, and then carrying out empirical observations to validate those formulated and stipulated conjectures. 

    The scientific method goes through the formation of a sequence of steps to reach from the knowledge pool to well-formulated derivations and formulae. It consists of the following crucial steps :

    1. Systematic Observations
    2. Controlled Experiments
    3. Qualitative and Quantitative reasoning
    4. Mathematical Modelings
    5. Prediction and verification of theories.
    6. Speculation or Prediction

    Physics and its scope

    Physics is the branch of science related to the study of basic laws of nature and their manifestations concerned with the different natural phenomena. It is also referred to as the “fundamental science” because it constrains all the other significant branches of the sciences. It can be considered to be the study of the physical world and matter along with its motion through space and time. It also pertains to the concepts of energy and force as well.

    Physics consist of two principal types of approaches :

    1. Unification- Different constraints are applied to all the phenomena occurring together as a collection of universal laws in different domains in the world. It is an attempt to unify various laws and combine to carry out an activity. It is based on trial and process. For instance, both electric and magnetic phenomena are governed by electromagnetic laws.
    2. Reduction- This approach is based on the principle of deriving the properties of complex systems from the interactions, dependencies, and properties of their constituent parts. It can be used to understand the working of complex systems. For instance, the temperature of a system is reduced to average kinetic.

    Scope of Physics

    The scope of physics spreads over both massive objects like the universe and its surroundings, as well as to negligibly small-sized particles, like electrons, protons, etc., It is vast as it converts quantities with varying lengths stretching over a magnitude as high as 1060 m (study of the universe) or as low as 10-12 m (study of electrons, protons, etc). It also encompasses a wide range of masses from minutely small, like protons, neutrons etc., 10-10 kg, to highly massive galaxies, 1080 kg. Physics considers both the microscopic and macroscopic domains.

    Physics is divided into two major categories based on its scope:

    1. Classical Physics: Deals with the macroscopic phenomena (mechanics, thermodynamics, and electromagnetism). It can be considered to be a sub-branch of applied mathematics. The laws of motion framed by Isaac Newton were designed and developed keeping in mind the principles of classical physics.
    2. Modern Physics: Deals with microscopic phenomena (Special Relativity, Quantum Mechanics).

    Some Branch of Physics

    1. Mechanics- The branch of physics dealing with the movement of physical objects, more specifically the relationships between force, matter, and motion associated between them. It takes into consideration the objects both at rest and in motion. 
    2. Electrodynamics- The branch of physics dealing with rapidly changing electric and magnetic fields. It also pertains to the understanding of the particle motion and interactions produced within the variable fields. Maxwell devised numerous laws that are concerned with the motion of electric fields and their attributes.  
    3. Optics- The branch of physics dealing with the behavior and the interactions of light with each other. It can be used to simulate the construction of devices used to visualize and detect the aspects and components of light. It takes into account both ray and wave optics. It involves concepts related to the formation of images and the working of topics of reflection, refraction as well as diffraction. 
    4. Thermodynamics- The branch of physics related to heat and energy and its involved concepts. It also described the relationship with radiation along with the physical properties of matter. It also includes the conversion of heat into different types of energy; mechanical or electrical energy.

    Physics in Relation to Other Sciences

    Physics is a very significant branch of science that plays a crucial role in understanding the developments pertaining to the other branches of science, such as Chemistry, Biology, etc.

    • Physics in relation to Mathematics. The study of physical variables involved in the study of mathematics has led to the discovery of ideas of differentiation, integration, and differential equations involved in the estimation of quantities. Theories in physics and derivations in mathematics coexist with each other. Math is considered to be a deterministic tool for the development of modern theoretical physics. It provides a way to formulate and evaluate experimental results.
    Mathematics  Physics
    Graph Represents a single object. Represents a relationship between two quantities.
    Axes Dimensionless numbers are represented by linear scaling Values of quantities are expressed in some units. Scaling may be linear or non-linear.
    Origin (0,0) Any arbitrary position.
    Plot range infinite The ranges of the quantities.
    Slope Gradient Dimensionless numbers have a geometric interpretation only. Change of one quantity with respect to another.
    • Physics in relation to Biology. Physics form the essence of the field of biology. The concepts and illustrations of space, time, and matter have induced a better understanding of the existence of living organisms and the study of the laws of conversation of energy. Many diseases and ailments have been better diagnosed over the years due to developments in physics and vice versa. Disease diagnosis has been very efficient due to X-ray invention and practices. 
    • Physics in relation to Chemistry. Chemistry is basically an extension of Physics. The concepts associated with X-ray diffraction and radioactivity have revolutionized the study of the periodic table. The intra-particle forces, as well as internal interactions, can also be used to get a better insight into the bonding and the chemical structure of substances. The structure, behavior, and properties of matter are both easily understood with both the branches existing together.
    • Physics in relation to Meteorology. Meteorology holds an explicit part in the discipline of physics. It tends to explain nature’s observed behavior through estimated hypotheses and conjectures while taking into consideration the various relativistic repercussions. Atmospheric physics and meteorology use both mathematical and physical models to understand the weather and climatic conditions. It also relates to the descriptive mathematical and computer modeling of atmospheric dynamics.   
    • Physics in relation to Astronomy. The branch of astronomy is considered to be applied physics since it applies the scientific hypotheses and basic rules of physics to further the understanding of the celestial bodies and universe.For instance, the discovery and usage of radio telescopes, as well as optical telescopes, have stipulated an easy way to explore the universe.
    Type of forces Governs 
    Gravitational force All objects in the universe
    Weak nuclear force Particularly electrons and neutrinos.
    Electromagnetic force Charged particles
    Strong nuclear force Nucleons, heavier elementary particles

    The other sciences, like geology, oceanology, seismology, etc, also use some laws of physics.

    Sample Problems

    Problem 1: What is “high-energy” physics? 

    Solution: 

    High-energy physics, which is also termed particle physics, refers to the study of the elementary constituents of matter and energy along with their corresponding interactions. Particle physics is concerned with the design and development of high-energy accelerators and detectors.

    Problem 2: Explain the relation of physics to seismology. 

    Solution: 

    Seismology is also referred to as the scientific study concerned with earthquakes and their related phenomena, such as volcanic eruptions. The movement of the earth’s crust, that is, the tectonic shifts and the types of waves emitting energy helps us in studying the earthquake and its repercussions.

    Problem 3: Differentiate between weak and strong nuclear forces. 

    Solution:

    The difference between weak and strong nuclear forces are as follows:

    Weak nuclear forces Strong nuclear forces
    It makes the radioactive particles decay. It keeps the protons and neutrons of a nucleus together.
    Weak and very short-ranged. Strong and short ranged.
    Example: Conversion of a proton to a neutron. Example: fusion process between stars and the sun.

    Problem 4: What is the difference between classical and modern physics? 

    Solution: 

    Classical physics deals with the study of objects on a macroscopic scale, which can be studied with the largely unaided five human senses. This is in comparison to modern physics, which is concerned with the nature and behavior of particles and energy at the sub-microscopic level. The laws of one branch of physics remain inapplicable to the other branch and vice versa. Also, most of the laws of classical physics are deterministic.

    Problem 5: Define astrophysics. 

    Solution: 

    Astrophysics is a branch of science dealing with the methods and principles deployed in the study of astronomical objects and phenomena of the universe.

    Problem 6: Explain the reasons behind the durability of scientific knowledge. 

    Solution: 

    • It is easily corroborated by multiple scientists working independently.
    • Consistent and accurate with different scientists.
    • Vast knowledge accumulating over many years.

    Problem 7: Is it possible to modify a scientific theory? 

    Solution: 

    A scientific theory can be revised if required to accommodate new phenomena or data. It is not fixed and can be reformulated.

    See less
W3spoint99
  • 0
W3spoint99Begginer
Asked: December 26, 2024In:
  • 0

What is Physics? Definition, History, Importance, Scope (Class 11)

atomselectricityenergyforcesgravitylaws of motionlightmagnetismmattermoleculesmotionphysicsquantum mechanicsrelativitysciencescientific discoveriesscientific methodsoundthermodynamicsuniverse
  1. Saralyn
    Saralyn Begginer

    The most curious mind out of all the species is the mind of homosapiens. Humans are always curious about the nature around them and the magic laws on which it functions. The sun always rises in the east and sets in the west, the moon appears at night and the sun appears in the day, and so on. All thRead more

    The most curious mind out of all the species is the mind of homosapiens. Humans are always curious about the nature around them and the magic laws on which it functions. The sun always rises in the east and sets in the west, the moon appears at night and the sun appears in the day, and so on. All these questions not on make humans curious but make them think and discover about the different theories of nature and by doing so, humans soon started discovering physics in order to discover the world and its mystery. Let’s learn what is physics in more detail,

    What is Physics?

    The word “science” has been originated from a word in the Latin dictionary named “Scientia” which means “to know”. Therefore, in one way, it can be said that science is nothing but to know the working of everything, from nature to machines. Under science, a category well known is nature science, which is the study of the physical world around humans. Physics, chemistry, biology, geology, all these fields lie under nature science.

    A basic discipline of nature sciences is physics. Physics is also a word taken from the Latin dictionary which means nature. In Sanskrit, it is known as “Bhautiki” which is the physical world around. The definition of physics is not accurately present but it can be said that physics is the study of all basic laws of nature and their manifestation in a different phenomenon.

    Physics as a whole explains the diverse physical phenomenon with respect to concepts and laws. For instance, from the falling off an apple on the ground and the law associated with it to the revolving of planets around the sun, to electromagnetism and its effects, physics defines it all. The major concept involved in physics is the use of basic approaches for bigger and complex problems, the process of solving a complex problem by breaking them into smaller parts is called reductionism. Then the act of unifying different laws is called unification.

    History of Physics

    The word science has been originated from a Latin word named “Scientia” which means “to know”. The word “Physics” has been originated from a Greek word named “Phusike” which means nature. In Sanskrit, physics is called “Vigyaan” which means “knowledge”, all of these words simply tell that physics is as old as the human species. Early civilizations like Egypt, India, Greece, etc, made a significant contribution in the field of physics. From the 16th century, Europe participated heavily and contributed. By the mid-twentieth century, science became an international enterprise and the rapid growth in the very field is on. The two major approaches in physics are already described above, they are unification and reductionism.

    Importance and application of physics

    • The complex and bigger magnitude identities are explained using simpler theories.
    • New devices are invented using the basic physics laws.
    • The observations and experiments can be used to create new laws or to modify the existing laws.
    • The ultimate aim is to find a unified set of laws that govern matter, energy, motion at both microscopic and macroscopic levels.

    Scope and Excitement of Physics

    The scope of physics can be majorly understood by looking at its sub-divisions. There are basically two types of studies in physics, macroscopic physics, and microscopic physics. Macroscopic physics deals with phenomena on a terrestrial, astronomical scale, while microscopic physics deals with the phenomenon on an atomic, molecular, or nuclear scale. The macroscopic study is done mostly in classical physics that includes subjects like mechanics, thermodynamics, etc. The microscopic study is the study of the structure of the atom, etc. Classical physics is unable to contribute in this field and currently, quantum theory is referred for the microscopic level studies.

    Therefore, it can be said that the scope of physics is really very vast. The study covers a plethora of physical quantities like length, mass, time, energy, etc. From the study of smallest quantities (ranging up to 10-30 or less) to the study of the quantities on an astronomical level (ranging up to 1020 or more).

    Fundamental forces in Nature

    Force is seen and experienced on a daily basis and is available on both macroscopic and microscopic levels. At a macroscopic level, apart from gravitational force, several kinds of forces are experienced, for instance, muscular force, contact forces, the elongation or compression of elastics, etc. On a microscopic level, there are electric and magnetic forces, nuclear forces, etc. Although, it was further observed that most of the forces defined or explained are derived from four fundamental forces. The four fundamental forces in nature are,

    • Gravitational Force: It is the mutual force that occurs between two objects by the virtue of their masses. Gravitational force is a universal force. The formula for gravitational force is,

    FG = (G M1M2)/r2

    FG = Gravitational force

    M1, M2 = Masses1 and 2.

    r = distance between the center of the masses.

    • Electromagnetic force: It is the force that occurs between the charged particles. If the charges are at rest, the phenomenon of electric field occurs and if the charges are moving, both electric and magnetic field phenomenon occurs. Therefore, it is named electromagnetic force.
    • Strong nuclear force: It is the strongest force among all four fundamental forces. This force binds the protons and neutrons in a nucleus. This force is charge independent, that is, it acts on proton-proton, proton-neutron, etc.
    • Weak nuclear force: Weak nuclear force is not the weakest force among fundamental forces. It is not as weak as a gravitational force but is weaker than the electromagnetic force. This force is observed in only some nuclear processes, for example, β-decay of the nucleus.

    Conceptual Questions

    Question 1: Which of the four fundamental forces is the weakest and the strongest?

    Answer: 

    The weakest force in nature is the gravitational force and the strongest force in nature is the strong nuclear force.

    Question 2: What are the laws of conservation in nature?

    Answer:

    Following are the laws of conservation in nature:

    1. Law of conservation of mass.
    2. Law of conservation of energy.
    3. Law of conservation of momentum.
    4. Law of conservation of charge.

    Question 3: On what two things the scope of physics is defined?

    Answer:

    The two things on which the scope of physics is defined are unification and reductionism. Unification is the physics of unifying all laws. Whereas, reductionism is the process of solving complex problems by breaking them into simpler parts.

    Question 4: What part of the study is not handled by the classical study of physics?

    Answer:

    The microscopic study of the physical world is not handled by classical physics. A new field termed quantum theory handles the study of physics at the microscopic level.

    Question 5: Give an example of a weak nuclear force.

    Answer:

    The weak nuclear force is observed in a few nuclear processes. An example of a weak nuclear force is the β-decay of the nucleus.

    See less